Table of Contents
What Magnitude & Sign of Charge Q will Make Force on Charge Q Zero?
Usually, whenever we need to solve any type of problem, we should first search. In this article, we want to explain what Magnitude and Sign of Charge Q will Make the Force on Charge Q Zero. Here so many ways to solve this problem.
To solve this problem, “What Magnitude and Sign of Charge Q will Make the Force on Charge Q Zero?” I searched google and found the Answers on many sites. But in this regard, I saw so many different types of Answers.
Here I will explain my experience. Let’s look into this!
Explanation
Expert Q&A – Chegg.com
When I opened this chegg.com, for this “What magnitude and sign of charge q will make the force on charge q zero?” question, they explained the answer below follows:
What is the Equipotential Surface?
After chegg.com, I search for brainly.com. Here also brainly.com explain what magnitude and sign of charge q will make the force on charge q zero. The point on a charge q will be 0 when it is located on an equipotential surface.
An equipotential surface is a surface that refers to where the electric potential is. Here the point is constant. It won’t change its position. In that, we can find the electric field can be 0 and the force on the charge also 0.
When the charge is in an equipotential surface at that time, the magnitude and sign of q do not affect the force. Irrespective of the charge’s volume or character, if it is located on an equipotential surface, it will knowledge no net power.
Question
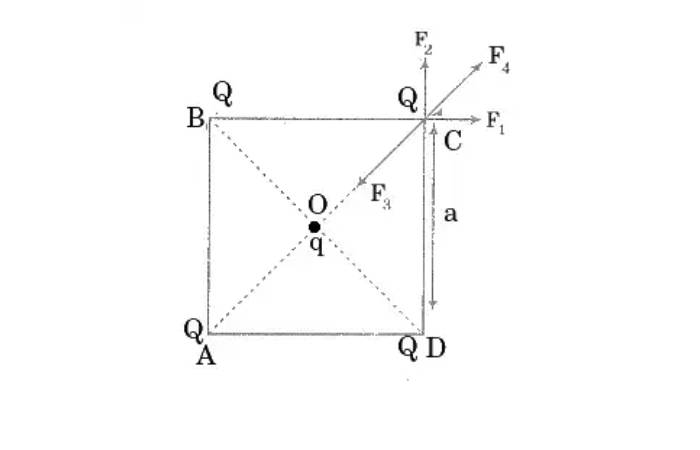
A square has a charge in the middle and four charges at each of the four corners that are each equal to Q. When the system is in equilibrium, q has the following value: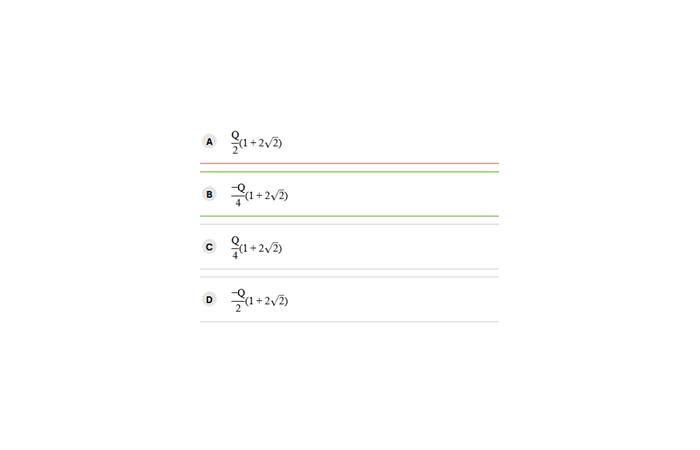
Solution – Correct option is B)
Step 1 : Calculate all the required distances between the charges :
side length of the square be .
Figure shows that in ACD, AD2+CD2=AC2.
AC=2 a2+a2=AC2 a2+a2=AC2 a2+a2=AC2 a2+a
OC=2AC =2, however.
Step 2: Central charge equilibrium
Because of the diagonally opposite charges cancelling each other, the force on the central charge will be equal and opposite.
To find the value of q, we must first check the equilibrium of any one charge at the corner.
Step 3: Force generated by all of the charges at point C – Sign of Charge
Force on charge at C as a result of B, F1 =a2KQ2
Force on charge at C as a result of D, F2 =a2KQ2
Force on charge at C as a result of A, F4 =AC2KQ2 =2a2KQ2
Because of the q in the centre, there is a force on charge at C.
F3=OC2KqQ=a22KqQ
Step 4: Put the equilibrium condition into action at C: Sign of Charge
To be in equilibrium, the net power substitute on charge at C must be zero.
As a result, F3 + F1 + F2 + F4 = 0.
Because (F1 = F2), the product of F1 and F2 (along OC, by symmetry) = F12 +F22 =2 F1
Also, because F3 and F4 are along OC, the magnitudes of the sum of these forces should be zero.
⇒ ∣F3∣+2\s∣F1∣+∣F4∣=0
a22KqQ + 2 a2KQ2 + 2a2KQ2 = 0
⇒2q=−(2\sQ+2Q)
⇒q=−4Q(1+22\s)